全连接神经网络（上）

全连接神经网络通过多个变换来实现输入到输出的映射

eg.两层神经网络：$f=W_2\max(0,W_1x+b_1)+b_2\quad(1)$

$W_1$也可看做模板，模板个数可以人为制定 而在线性分类器中，$W$为模板，个数就是类别个数

$W_2$融合多个模板匹配结果实现最终打分

线性评估$\to$非线性操作$\to$线性评估$\to…$

全连接神经网络可用于解决线性不可分问题

1.绘制与命名

输入层、隐层、输出层

2.激活函数

如果缺少激活函数，神经网络会退化为线性分类器

1. sigmoid函数 $f(x)=\frac{1}{1+e^{-x}}$
2. tanh函数 $f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
3. relu函数$f(x)=\max(0,x)$
4. leaky relu函数$f(x)=\max(0.1x,x)$

神经元个数越多，分界面越复杂，在集合上分类能力越强

3.损失函数

softmax（将分数转换为概率）

在得出最终评估分数后将分数指数化（$e^{score}$）$\to$归一化（$\frac{t_j}{\sum_{j}t_j}$）$\to$概率

交叉熵损失

• 熵 $H(p)=-\sum_{x}p(x)\log^{p(x)}$
• 交叉熵 $H(p,q)=-\sum_{x}p(x)\log^{q(x)}$
• 相对熵 $KL(p||q)=-\sum_{x}p(x)\log^{\frac{q(x)}{p(x)}}$——度量概率分布间的不相似性
• 关系$H(p,q)=H(p)+KL(p||q)$

由于真实概率分布一定为一个独热向量（one-hot vector），即一个维度为1，其余维度均为0的概率分布向量，因此$H(p)$一定为0，因此在全连接神经网络中交叉熵$H(p,q)$等于相对熵$KL(p||q)$，即：$-\sum_{i=1}^{c}p(x_i)\log{q(x_i)}=-\log{q_j}$其中j为真实类别的预测概率

对比多类支撑向量机损失

多类支撑向量机损失：只高一分即可，高于一分则认为没有损失

交叉熵损失：正确概率越高越好，错误越低越好

4.优化算法

计算图与反向传播

计算图是一种有向图，它用来表达输入、输出以及中间变量间的计算关系，图中的每个节点对应一种数学运算

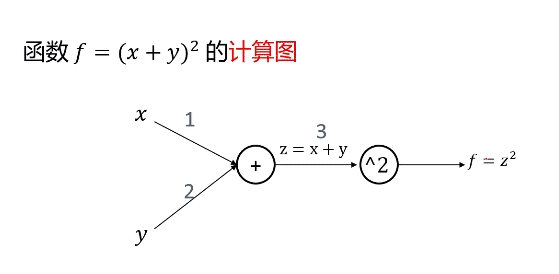
反向传播算法——利用链式法则，将上游梯度同当前节点求导出的局部梯度相乘

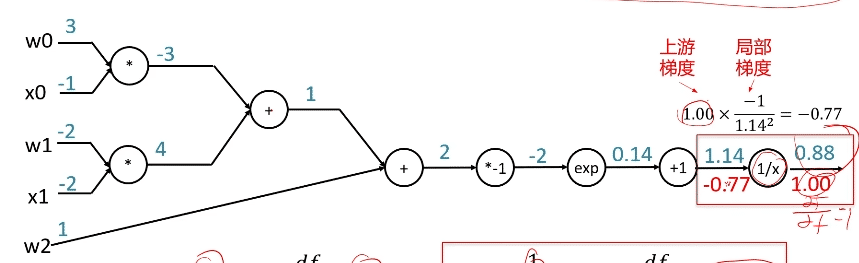
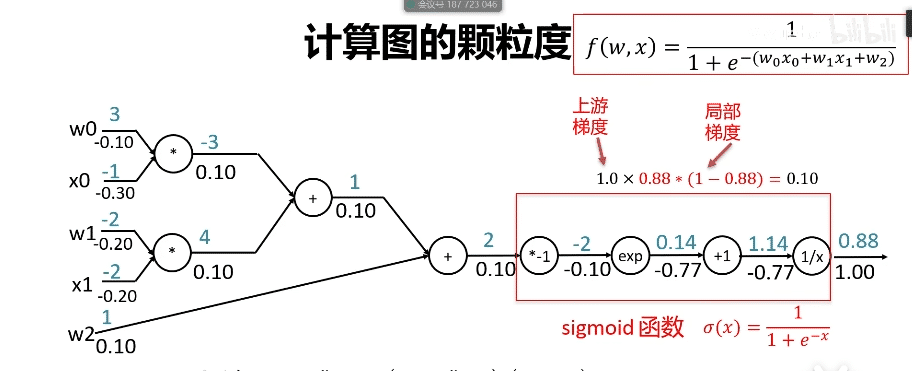
总结

1. 任意复杂函数均可使用计算图表示
2. 每个门单元需进行如下计算：
   1. 计算输出
   2. 计算其输出关于输入的局部梯度
3. 利用链式法则，门单元将会回传的梯度乘以对其输入的局部梯度，从而得到整个网络输出对于该门单元的梯度

问题：链式法则使得梯度不断向乘，可能导致梯度消失

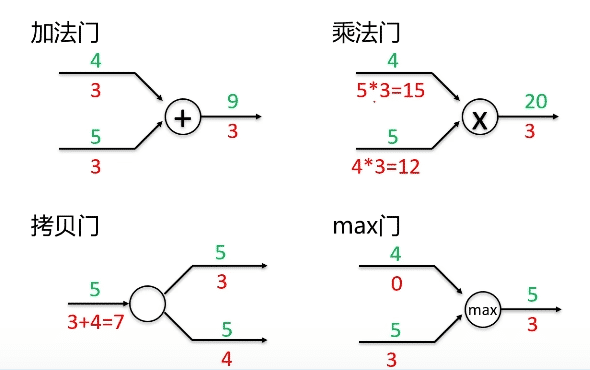
常见门单元及其回传梯度